Ratkaistu: / tehtävää

Lukujärjestelmät

Nämä tehtävät eivät vaikuta arvosanaan.
Tässä apumateriaalissa esitellään kurssilla tarvittavien lukujärjestelmien perusteet, eli miten eri tavoilla luvut voidaan esittää. Kymmenkantaiset luvut ovat kaikille tuttuja peruskoulumatikasta, mutta muut kannat voivat olla tulleet vastaan vasta yliopistossa tai ei lainkaan. Esimerkit tässä materiaalissa on tehty Pythonilla, jotta niitä voi ajaa helposti
interaktiivisessa tulkissa
.
Osaamistavoitteet: Tämän materiaalin läpikäytyäsi ymmärrät mitä ovat binääri- ja heksadesimaaliluvut sekä osaat muuttaa lukuja kannasta toiseen. Lisäksi tiedät miksi nämä muut kannat ovat kurssilla tarpeellisia. Lisäksi osaat pyöritellä bittioperaatiota Python-tulkissa.

Valitse kantasi

Kuten todettua, ns. normaalit kokonaisluvut joilla on laskettu peruskoulusta lähtien ovat kymmenkantaisia. Olemme oppineet tulkitsemaan kymmenkantaisia lukuja nopealla vilkaisulla: osaamme nopeasti todeta, että 156 on sataviisikymmentäkuusi. Tämän luvun voi kuitenkin muodostaa myös systemaattisesti sen yksittäisistä numeroista käyttämällä kantalukua, joka on siis 10. 
>>> 6 * 10 ** 0 + 5 * 10 ** 1 + 1 * 10 ** 2
156
Ylläoleva on matemaattinen kuvaus sille, että kymmenkantaisessa järjestelmässä oikeanpuolimmaisin kertoo ykköset, sitä seuraava kymmenet ja sitä seuraava sadat jne. Purkaminen oikealta vasemmalle on helpompaa, koska silloin voidaan asettaa eksponentti nollaan ja kasvattaa sitä yhdellä kun siirrytään eteenpäin. Lukua ei nyt siis ajatella kokonaisuutena, vaan yksittäisistä numeroista muodostuvana summana. Tällöin kunkin numeron kohdalla kerrotaan numero kantaluvulla, joka on korotettu potenssiin i, jossa i on numeron paikka luvussa (oikealta laskettuna, alkaen nollasta). Sama esitettynä Python-koodilla jos jollekin koodi kertoo enemmän kuin sanallinen selitys: 
luku = "156"
summa = 0
for i, numero in enumerate(luku[::-1]):         # [::-1] = käydään läpi oikealta vasemmalle
    summa += int(numero) * 10 ** i              # kasvatetaan summaa
    
print(summa)                                    # tulostaa 156
Tässä koodissa esiintyvä numeroarvo 10 on siis kanta. Se kertoo myös mitkä ovat sallittuja numeroja luvussa: 0, 1, ..., 9. Eli sallittuja ovat toisinsanoen väli [0:kanta-1]. Tämä systemaattinen purkamistapa on tärkeä, koska ihmiset eivät ole hyviä lukemaan muihin kantoihin kuuluvia lukuja silmämääräisesti - ainakaan ilman harjoitusta! Kanta tarkoittaa myös sitä, että jos luvun numeroja siirretään (shift) vasemmalle, saadaan aikaan kertominen kantaluvulla - vastaavasti jos niitä siirretään oikealle saadaan aikaan jakaminen kantaluvulla. Tämä on helppo nähdä jos otetaan luku joka päättyy nollaan ja lisätään lisäksi etunollia: 
>>> luku = "00310"
>>> int(luku)
310
>>> luku = "03100"          # siirretty kerran vasemmalle
>>> int(luku)
3100
>>> luku = "00031"          # siirretty kerran oikealle (alkuperäisestä)
>>> int(luku)
31

Binääriluvut

Binääriluvut
ovat keskeisiä kun käsitellään tietokoneita. Tämä johtuu siitä, että tietokone käsittelee pelkkiä
bittejä
- siis nollia ja ykkösiä. Sattumoisin binääriluku on nimitys kaksikantaisille luvuille - kantaluku on siis 2, ja täten edellisen perusteella sallitut numerot ovat 0 ja 1. Binääriluvun suuruus muodostuu samalla idealla kuin yllä esitetty kymmenkantaisen luvun purkaminen. Nyt vain kymppien tilalle tulee 2. Esimerkkilukuna olkoon vaikka 1011. 
>>> 1 * 2 ** 0 + 1 * 2 ** 1 + 0 * 2 ** 2 + 1 * 2 ** 3
11
Periaatteessa nollalla kertomisen voi jättää pois, mutta kokonaisuuden ymmärtäisen kannalta on parempi nähdä jokaisen numeron purku. Koodilla tämän voisi purkaa ihan samalla periaatteella: 
luku = "1011"
summa = 0
for i, numero in enumerate(luku[::-1]):         # [::-1] = käydään läpi oikealta vasemmalle
    summa += int(numero) * 2 ** i               # kasvatetaan summaa (huom. 10 vaihtunut 2:ksi!)
    
print(summa)                                    # tulostaa 11
Koska tietokoneen sisällä tyypillisesti puhutaan rajallisista bittimääristä, kukin luku myös esitetään tietyllä bittimäärällä. Tämä kertoo miten monta eri arvoa binääriluvulla voidaan esittää. Erillisten arvojen lukumäärä on yksinkertaisesti 2 ** n jossa n on bittien lukumäärä. Aina kun lisätään yksi bitti, esitettävien arvojen määrä kaksinkertaistuu. Huomattavaa on myös, että koska 0 on olemassa, suurin arvo joka voidaan esittää N-bittisillä binääriluvulla on 2 ** n - 1.
Binäärilukuja esittäessä tulee tietää bittien järjestys binääriluvussa. Ts. kun meillä on bittijono 11101, mitenpäin se luetaan? 
Miten tulkitaan binääriluku 11101 kymmenjärjestelmän lukuna??
10111 -> 23
11101 -> 29
Kymmenjärjestelmää olemme tottuneet ymmärtämään niin, että ensimmäinen luku ilmaisee suurimman kantaluvun potenssin ja sen kertoimen. Esim. luvussa 156, numero ensimmäinen numero on 1*(10**2). Emmekä käsitä lukua niin, että suurin potenssi olisi oikeanpuolimmaisin luku, eli 6*(10**2).
Samoin tietokoneelle pitää kertoa kummin päin luku luetaan, eli bittijärjestys. Mikä bitti on pienin kakkosen potenssi eli vähiten merkitsevä bitti (engl. least significant bit, LSB)?? Ja vastaavasti suurin kakkosen potenssi eli eniten merkitsevä bitti (engl. most significant bit, MSB)??
No, päätämme asian kurssin osalta tässä ja nyt. Materiaalissa tästä eteenpäin MSB on vasemmanpuoleisin bitti, eli ymmärrämme binääriluvun samoin kuin kymmenjärjestelmän luvut.

On olemassa 10 ihmistyyppiä...

...ne jotka osaavat lukea binääriä ja ne jotka eivät. Ok, vanha vitsi. Selvitetään kuitenkin kumpaan ryhmään sinä kuulut! Tämä tehtävä kannattaa tehdä kynän ja paperin kanssa jolloin se jopa auttaa ymmärtämään binäärilukuja. Alla on muutamia binäärilukuja: 
1101111
1011011010
0101010
010
Kirjoittele vastaavat luvut 10-kantaisina tekstilaatikkoon alekkain
Varoitus: Et ole kirjautunut sisään. Et voi vastata.

Heksadesimaaliluvut

Ihmiset ovat siis tottuneet lukemaan kymmenkantaisia lukuja ja tietokoneet kaksikantaisia. Näiden kahden järjestelmän välillä on kuitenkin ongelma: koska 10 ei ole kakkosen potenssisarjassa, kymmenkantaisesta luvusta ei suoraan nähdä montako bittiä sen esittämiseen tarvitaan, eikä siitä ole helppo muuntaa
binäärilukua
- sitä ei myöskään voida helposti jakaa lohkoihin (ei voida suoraan sanoa mitkä
bitit
tuottavat kunkin yksittäisen numeron). Esimerkiksi luvuissa 255 ja 256 ovat näennäisesti samaa suuruusluokkaa, mutta toisen voikin esittää 8 bitillä siinä missä toiseen tarvitaan 9. Toinen ongelma liittyy binäärilukujen vertailuun. Pikakysymys - onko tässä kaksi samaa lukua: 1011001101001011 1011001101101011? Binääriluvut ovat luonnostaan todella pitkiä ja niiden parsinta on silmille hankalaa.
Näistä syistä käytämme kompromissina
heksadesimaalilukuja
. Näissä luvuissa kantana on 16, ja esitystapa muodostuu siten, että numerot 10...15 korvataan kirjaimilla A...F.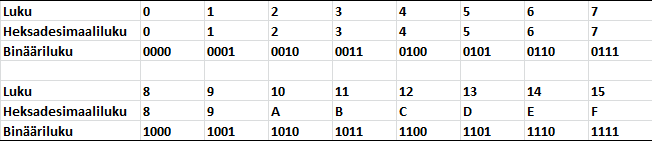
Heksadesimaaliluvut
Heksoina esitettynä em. binääriluvut olisivat b34b ja b36b, joista on huomattavasti helpompi nähdä, että kyseessä on kaksi eri lukua. Lisäksi niistä nähdään myös nopeasti, että lukujen erotus on 20 eli 10-kantaisena 2 * 16 ** 1 (32). Vieläkin hyödyllisempää on, että yksi numero heksaluvussa vastaa tasan neljää bittiä: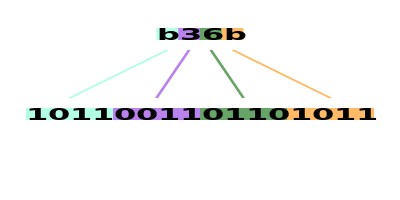
heksadesimaaliluku ja sen numeroita vastaavat bitit
Heksaluvusta nähdään siis suoraan mitkä bitit ovat muuttuneet kun verrataan kahta arvoa. Tämä on elämää helpottava ominaisuus kun tehdään
bittioperaatiota
.
Muunnos kymmenkantaiseksi menee tuttuun tapaan kunhan muistetaan mitä lukuja kirjaimet vastaavat. 
>>> 11 * 16 ** 3 + 3 * 16 ** 2 + 6 * 16 ** 1 + 11 * 16 ** 0
45931

Binäärikirous

Tässä tehtävässä puretaan heksadesimaalilukuja binääreiksi. Alla on siis esitetty nippu 16-kantaisia lukuja ja tehtäväsi on taikoa niistä binäärejä. Homma onnistuu helpoiten yksi numero kerrallaan kun vielä muistaa että 0...f on binäärinä 0000...1111. Muista merkitä myös etunollia vastaavat bitit! Tämäkin tehtävä kannattaa tehdä kynän ja paperin kanssa. 
f3c1
0917
aa51
Kirjoittele vastaavat binääriluvut allaolevaan laatikkoon.
Varoitus: Et ole kirjautunut sisään. Et voi vastata.

Muunnokset toiseen suuntaan

Tässä käymme lyhyesti läpi miten 10-kantainen luku muunnetaan binääriksi ja heksadesimaaliksi. Aloitetaan muunnoksella 10-kantaisesta 2-kantaiseen. Menetelmässä tuotetaan bitit oikealta vasemmalle, eli pienin bitti saadaan ensimmäisenä. Menetelmä etenee siten, että luku jaetaan aina kahdella, ja jakojäännös merkitään binäärilukuun kun taas osamäärä jatkaa seuraavalle kierrokselle, missä se puolestaan jaetaan kahdella ja merkitään jälleen jakojäännös ylös. Jatketaan kunnes osamäärä on 0. Olkoon luku 125, jolloin koko prosessi menee:
  1. Jaetaan 125 / 2 -> osamäärä 62, jakojäännös 1 -> binääriluku on nyt '1'
  2. Jaetaan 62 / 2 -> osamäärä 31, jakojäännös 0 -> binääriluku on nyt '01'
  3. Jaetaan 31 / 2 -> osamäärä 15, jakojäännös 1 -> binääriluku on nyt '101'
  4. Jaetaan 15 / 2 -> osamäärä 7, jakojäännös 1 -> binääriluku on nyt '1101'
  5. Jaetaan 7 / 2 -> osamäärä 3, jakojäännös 1 -> binääriluku on nyt '11101'
  6. Jaetaan 3 / 2 -> osamäärä 1, jakojäännös 1 -> binääriluku on nyt '111101'
  7. Jaetaan 1 / 2 -> osamäärä 0, jakojäännös 1 -> binääriluku on nyt '1111101'
Python-silmukkana: 
binaari = ""
luku = 125
while luku > 0:
    luku, bitti = divmod(luku, 2)           # Lasketaan osamäärä ja jakojäännös
    binaari = str(bitti) + binaari          # Huom: muista liittää uusi numero luvu *alkuun*
    
print(binaari)
Vähemmän yllättäen prosessi etenee samalla tavalla heksadesimaaliluvuksi muunnettaessa, mutta jakajana on tietenkin kantaluku 16. Otetaan hieman suurempi luku, 4451.
  1. Jaetaan 4451 / 16 -> osamäärä 278, jakojäännös 3 -> heksadesimaaliluku on nyt '3'
  2. Jaetaan 278 / 16 -> osamäärä 17, jakojäännös 6 -> heksadesimaaliluku on nyt '63'
  3. Jaetaan 17 / 16 -> osamäärä 1, jakojäännös 1 -> heksadesimaaliluku on nyt '163'
  4. Jaetaan 1 / 16 -> osamäärä 0, jakojäännös 1 -> heksadesimaaliluku on nyt '1163'
Vastaava Python-silmukka:
heksa = ""
luku = 4451
while luku > 0:
    luku, bitti = divmod(luku, 16)           # Lasketaan osamäärä ja jakojäännös
    heksa = str(bitti) + heksa              # Huom: muista liittää uusi numero luvu *alkuun*
    
print(heksa)

Muunnosrutiini

Debugatessa laiteläheisiä ohjelmia arvot näkyvät monesti heksadesimaalina tai binäärinä. Harjoitellaan siis numeroiden muuntamista binäärin, desimaalin ja heksadesimaalin välillä! Jokainen muunnos pitää saada oikein vain kerran.
Vinkki: Nämä tehtävät voi halutessaan tehdä Pythonilla.

Varoitus: Et ole kirjautunut sisään. Et voi vastata.

Muunnokset Pythonissa

Python-tulkki
on kätevä työkalu erikantaisten lukujen pyörittelyyn. Tässä käymme lyhyesti läpi miten sillä muunnetaan lukuja kannasta toiseen.
Binäärilukuja
voi kirjoittaa Python-tulkkiin laittamalla luvun alkuun 0b merkiksi siitä, että luku on tulkittava 2-kantaisena:
>>> 0b1011
11
Samaten Pythonissa saa helposti esiin binääriesityksen kokonaisluvulle bin-funktiolla:
>>> bin(11)
'0b1011'
Python ei suoranaisesti tue muita kuin kymmenkantaisia lukuja, joten nämä esitystavat talletetaan merkkijonoihin. Binääriluvun voi myös lukea merkkijonosta käyttämällä int-funktiota lisäargumentilla, jolla kerrotaan merkkijonossa olevan luvun kanta: 
>>> int("1011", 2)
13
Vastaavasti
heksadesimaaliluku
voidaan syöttää Pythoniin 0x-etuliitteellä:
>>> 0xb36b
45931
Tai käyttämällä int-funktiota lisäargumentilla:
>>> int("b36b", 16)
45931
Toiseen suuntaan muunnoksen voi tehdä hex-funktiolla:
>>> hex(45931)
'0xb36b'

Lopuksi

Eipä muuta tältäosin, takaisin itse pääasiaan!
?