LAB_DICT: STL, Maps, and Iterators¶

Due date: 2024-04-22 23:59.

Assignment Description¶

This lab is all about making you think with dictionaries. Dictionaries (aka maps or associative arrays) are an abstract data type (ADT) which stores pairs of data and can support operations like insert, find, and remove. We generally call these (key, value) pairs. The idea is to associate a key with a certain value. Hence, dictionaries are useful for when you want to quickly “lookup” a value associated with a certain key. The name dictionary comes from the more familiar physical dictionary, where you lookup the definitions of words. If we were to model a physical dictionary with an ADT dictionary the keys would be the words, and the values would be their definitions.

Since dictionaries are abstract in nature, they have no prescription for what underlying structure should be used to implement them. Common choices are tree-based structures (e.g. balanced binary search trees, BTrees, etc.) or some sort of hash table. Different underlying implementations have different performance considerations, and which you use in the real world will depend on things like desired performance and what is readily available.

All Glory To The STL and C++11¶

In this lab we aren't making you implement a dictionary. Instead, you will be using dictionary types which have already been defined for you. In C++ there are two “built-in” dictionary types: map and unordered_map. Both exist in the wonderful land of the Standard Template Library (STL). The STL is a subset of the C++ Standard Library (the library a compiler must implement to be standard-compliant) which provides data containers. As the name implies, these containers are generic (templated) and thus can contain any type (which meets the restriction of the container). You've probably experienced at least one of the STL types so far: vector, which is pretty much just a super fancy array. In general, the STL types are very convenient as they provide a lot of functionality (e.g. sorting) that you don't have to bother implementing yourself.

Easy Type Declaration with ''auto''¶

Most of the stuff we present in this class uses old (C++03) style, but in this lab we encourage you to use some C++11 features to make your life easier.

The first helpful C++11 tidbit we'll talk about is auto. STL functions are really big on iterators and templates. Unfortunately, these types can get quite verbose. For example, if you have an unordered_map<int, string> (which maps an integer key to a string value) called m and you want to get the value associated with 5 (if it exists), you have to do something like this:

int key = 5;
unordered_map<int, string> m;
unordered_map<int, string>::iterator lookup;

/* Returns an iterator to a pair. */
lookup = m.find(key);
/* If the key isn't in the map, end() is returned. */
if(lookup != m.end())
    /* We access the second value in the pair pointed to by the iterator with ->second. */
    cout <<lookup->second <<endl;
else
    cout <<"Key " <<key <<" not found." <<endl;

Check out the type of lookup. It’s type is unordered_map<int, string>::iterator. Yikes. The trouble with the STL is that every time we want an iterator we have to specify the full type of the container and then add ::iterator. This can get pretty annoying. Thankfully, in C++11, there's auto. Instead of the above, you could do this:

int key = 5;
unordered_map<int, string> m;

/* Returns an iterator to a pair. */
auto lookup = m.find(key);
/* If the key isn't in the map, end() is returned. */
if(lookup != m.end())
    /* We access the second value in the pair pointed to by the iterator with ->second. */
    cout <<lookup->second <<endl;
else
    cout <<"Key " <<key <<" not found." <<endl;

Instead of explicitly specifying the type of lookup, we now say auto lookup. auto replaces the type information and does something called “type inference”. What this means is that the compiler will look at the type of the expression on the right hand side of the assignment and “fill in” the type information of the variable for you. Cool stuff, right? This means that for things like find we don't have to type out the nasty iterator type information. Now, don't go crazy with auto. A good rule of thumb is to only use it when it makes your code more readable. Since things like STL objects are pretty common it's often nice to use auto when dealing with functions that return iterators. For this lab we recommend you type out the full type information the first few times (just so that you remember what the actual type is) and then after that use auto.

Warning: Avoid excessive use of auto. While auto can be convenient, using it excessively without explicitly specifying types can make the code harder to understand and maintain. Use auto only when the type is clear and obvious. Also, consider indicating type information in the variable name when using auto. For example, using lookup_itr for an iterator variable.

Easy Element Access with ''operator[ ]''¶

Another convenient way to access elements in a map is with operator[] (just like array subscripts). However, you have to be careful. If key doesn't exist in a map m, calling an m[key] will create a default value for the key, insert it into m, and then return a reference to it. Because of this, you can't use [ ] on a const map.

Easy Iteration with Range-Based Loops¶

The next super cool thing in C++11 useful for this lab is range-based for loops. As it turns out, a lot of programs involve iterating over collections of data (e.g. an array) and doing something with each of those values. The duty of a programming language is to make programming easier for us humans, so there's usually some sort of construct in the language to accomplish this. In C++03 the main construct was for loops with iterators. So if you had a map<int, string> m; and you wanted to iterate over every (key, value) pair you would have to do something like this:

map<int, string> m;
map<int, string>::iterator it;
for(it = m.begin(); it != m.end(); it++)
    cout <<it->first <<", " <<it->second <<endl;

We can cut down on the verbosity in C++11 with some auto, but there's an even better way; what's called a “for each loop” or “range-based for loop”:

map<int, string> m;
for(std::pair<const int, string> & key_val : m)
    cout <<key_val.first <<", " <<key_val.second <<endl;

The way you should read that for loop is: “for each key_val in m do ...”. What's happening is that the for loop will update the variable key_val in each iteration of the loop to be the “next” element.

Since we are iterating over a map, the elements are (key, value) pairs. And we could use auto to even more simplify the syntax:

map<int, string> m;
for(auto & key_val : m)
    cout <<key_val.first <<", " <<key_val.second <<endl;

Notice that we use & in front of key_val. The type of key_val isn’t an iterator: it’s the “dereferenced” value of an iterator, in this case a reference to a std::pair<const int, string>. This value is a reference for two reasons: (1) so we don’t make useless copies, and (2) so we can modify the values in the map.

These kinds of for loops are simple, convenient, and intuitive to use. They have their limits, but for many iterating applications in C++ they're probably the best choice.

Warning: Always consider whether you need to iterate through your map or if you can use the find function, which is MUCH faster than iterating if you just need to access specific entries of your map. That being said, iterating is an important tool that you will need.

Download The Provided Files¶

Start with downloading and unzipping the provided files from here: lab_dict.zip.

1. Common Words¶

The first part of this assignment involves implementing an object called CommonWords that can find common words in different files.

There are three member functions: init_file_word_maps, init_common, and get_common_words, that are left for you to finish. init_file_word_maps and init_common functions serve as helpers for the main get_common_words function. These functions should initialize the necessary data structures and provide the required information to implement get_common_words.

init_file_word_maps initializes the private variable of the CommonWords class vector< map<string, unsigned int > > file_word_maps. This variable is a vector of maps, that for each file holds a map between words and their corresponding frequencies.
init_common initializes the private variable of the CommonWords class std::map< std::string, unsigned int > common. This variable is a map between the words and the number of files they occur in.

More details about these functions can be found in the common_words.h file.

Your ultimate goal is to properly implement get_common_words function which takes a number n as an input and finds all words that appear in every listed file at least n times. It should output a vector of such words, vector<string> out.

Hint: You can think of the words as keys, and their frequencies in each file are values (using an associative structure). However, you can implement get_common_words function in a number of different ways, but we provided you with the intermediate helper functions init_file_word_maps and init_common as one way of implementing it. If a different way of using maps and other structures seem more intuitive to you, feel free to do that instead.

Make sure you refer to the file named find_common_words.cpp to see how the main function utilizes the CommonWords class. Once your code is ready, you can compile it with:

make find_common_words

The resulting executable, named find_common_words, will allow you to find words that appear at least n times in all of the listed text files. The usage of the find_common_words executable is as follows:

./find_common_words [TEXT FILES] -n [NUM] -o [FILE]

You can further test it on the small text files or even novels provided for you in the lab_dict directory:

./find_common_words PrideAndPrejudice.txt Beowulf.txt SherlockHolmes.txt -n 500
and
in
of
the
to
./find_common_words small1.txt small2.txt -n 3
dog
pig

2. Anagrams¶

The second part of this assignment focuses on creating a dictionary that can look up anagrams of a given word. Anagrams are words that can be formed by rearranging the letters of another word. For example, "dog" and "god" are anagrams of each other.

Your task is to implement the AnagramDict class, which has a private variable called dict serving as this anagram dictionary. The dict map associates each word (key) of type string with a list of anagrams (value) of type vector of strings.

In the provided anagram_dict.h file, you'll find the definition of the AnagramDict class, which includes two unfinished constructors and two unfinished functions. Your task is to complete all of them.

The constructors: AnagramDict class should be constructed from a provided word list. The word list can be provided either as a vector or from a file (see words.txt). You MUST implement both constructors for the autograder to work!
The function get_anagrams takes a word as input, and returns a list of all the anagrams found in the word list. For instance, if you feed it the word "dog", it should return both "dog" and "god".
The function get_all_anagrams should simply print out the dict map values for those words that have at least one anagram (other than itself) in the word list. (That is, their value in the map dict should contain at least two words.)

Solving this task is a bit of a puzzle. It involves finding a clever way to uniquely identify groups of words that are anagrams of each other. To do this, we need to come up with a "key function" that ensures the same list of anagrams is returned when looking up different variations of a word. That is, a "key function", denoted as f, such that f("dog") == f("god"), f("silent") == f("listen") == f("tensil"), but f("dog") != f("silent"). This will ensure that we identify the groups of words that are anagrams of each other by looking up the value of this "key function" for any of the words. Hint: Take a closer look at the #include statement in anagram_dict.cpp.

One of the AnagramDict constructors takes a word list file name, which is expected to be a newline-separated list of words (in our case it is words.txt). To read this file you'll need to know some basic C++ file I/O. This following snippet will print out every word in such a word list file:

ifstream words(filename);
string word;
if(words.is_open()) {
    /* Reads a line from words into word until the file ends. */
    while(getline(words, word)) {
        cout <<word <<endl;
    }
}

Warning: When populating the dictionary with a set of words, be careful not to create duplicates. Our autograder won't let you pass if you overlook this!

To test your dictionary you can compile the anagram_finder by typing make anagram_finder. It will build the AnagramDict object from the word list provided by words.txt. Example usage / output:

./anagram_finder dog
Anagrams for dog:
dog
god

You can run it with the flag -a to print out a list of all the known anagrams for this word list. -o will redirect the output to a file, e.g.

./anagram_finder -a -o anagrams.txt

You can diff your output of the above command with all_anagrams_soln.txt. You may also specify your own word list file with -w if you're feeling adventurous (it defaults to words.txt in the current directory).

3. Pronunciation Puzzler¶

For this part of the lab you'll complete an object which will help solve the following puzzle taken from CarTalk:

"This was sent in by a fellow named Dan O'Leary. He came upon a common one-syllable, five-letter word recently that has the following unique property. When you remove the first letter, the remaining letters form a homophone of the original word, that is a word that sounds exactly the same. Replace the first letter, that is, put it back and remove the second letter and the result is yet another homophone of the original word. And the question is, what's the word?

Now I'm going to give you an example that doesn't work. Let's look at the five-letter word, wrack. W-R-A-C-K, you know, like to “wrack with pain”. If you remove the first letter, you are left with a four-letter word, R-A-C-K. As in, “Holy cow, did you see the rack on that buck! It must have been a nine-pointer!” It's a perfect homophone. If you put the ‘w’ back, and remove the ‘r’, instead, you're left with the word, wack, which is a real word, it's just not a homophone of the other two words.

But there is, however, at least one word that Dan and we know of, which will yield two homophones if you remove either of the first two letters to make two, new four-letter words. The question is, what's the word?"

In summary, we’re looking to find words such that:

the word itself,
the word with its first character removed, and
the word with its second character removed

are all homophones (i.e., have the same pronunciation) of each other. In addition, unlike this example, we are looking for words that are at least 5 characters long.

To accomplish this we are going to employ the help of CMU's Pronouncing Dictionary. The data associated with that dictionary is stored in a file (cmudict.0.7a) and read in on construction of a PronounceDict object (see pronounce_dict.h). You don't have to worry about the constructors this time since they're not very interesting. Instead you're responsible for writing the homophones function which determines whether two words are homophones or not. Check out pronounce_dict.h to see what kind of dictionary structure you're working with, and remember that it is mapping a word to its pronunciation.

PronounceDict expects the words to be uppercase. Here's some lovely code to transform a string str to uppercase:

std::transform(str.begin(), str.end(), str.begin(), toupper);

If you're wondering what transform is and where this toupper is coming from, transform applies the given function to a range and stores the result in another range (although in this case we store in the same location), and the function we use is toupper, which is defined in the global namespace by the cctype library.

Next you will have to write the code which actually solves the puzzle. This function resides in cartalk_puzzle.cpp. It takes a word list file name (similar as before, words.txt) and a PronounceDict. Things like the string class's substr function will probably prove useful. If all goes well you should be able to make it and run the executable with:

make homophone_puzzle
./homophone_puzzle

If you want to debug with cout, do not type using namespace std; since there would be some errors. For example, the toupper function we want to use is the one in global namespace, but there is another one in std namespace. You can type using std::cout and using std::endl if you wish, however.

There should be 5 resulting triples of words, but only one which matters. The answer CarTalk was looking for is probably the only one in the list where the two homophones are distinct (it doesn't matter for us if you don't make sure the homophones are distinct).

4. Memoization¶

Memoization is a clever trick that helps avoid repetitive work, by storing past results in a dictionary so they don't need to be calculated again. It's like having a function with a photographic memory. Whenever it's called with the same inputs, it goes, "Hold on, I've seen this before! Let me grab the answer from my secret stash." It checks if the result is already stored in the dictionary. If the answer is there, it happily returns it. But if it's not, only then it performs the calculation, saving the result in the dictionary for future reference. This way, memoization saves time by reusing past knowledge instead of starting from scratch each time.

You can read more about memoization on Wikipedia.

To demonstrate the benefits of memoization, we'll optimize computations of a recursive function using this technique. The Fibonacci numbers serve as a perfect example for this demonstration, because they are recursively defined as follows:

F(n) = F(n-1) + F(n-2);
F(0) = 0;
F(1) = 1.

If you draw out some trees for calculating these numbers (which we highly recommend) you'll notice something interesting. For example here is such a tree for F(6):

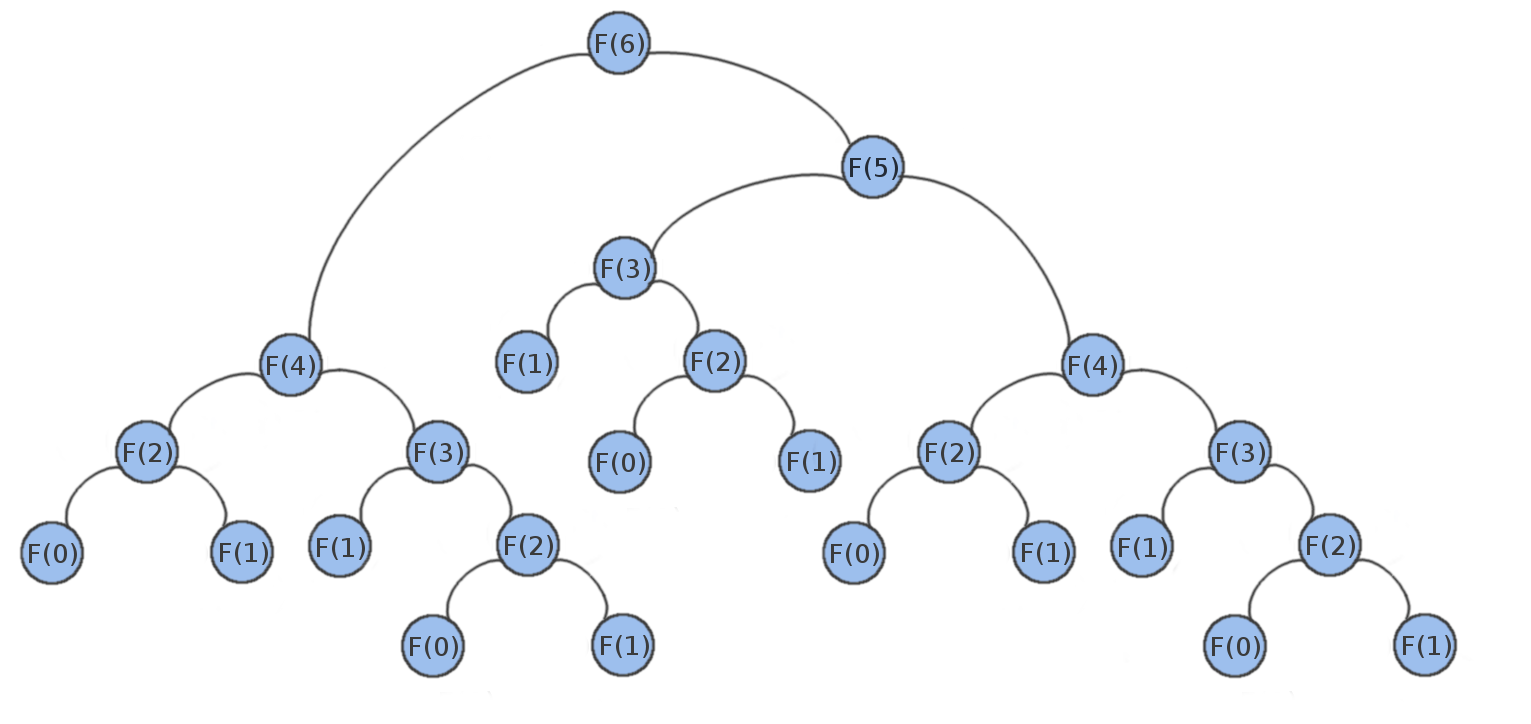
There's quite a bit of repetition in this tree. Specifically the entire F(4) subtree appears twice in the tree, as does F(3). The values in those trees get calculated twice. For larger values of n, the tree naturally gets larger and so do the repeated subtrees. Remember that the nodes in this tree represent function calls, so each one takes some time. Suppose the F(4) call on the right happens before the F(4) call on the left. By the time we get to the F(4) call on the left, we already knew the value of F(4). What if we could store the result of F(4)? If we stored it, then when we call F(4) on the left we don't need to bother with going through that entire subtree.

Now we will show how to use a dictionary to optimize the computation of Fibonacci numbers. In our memoized F function, we associate each input number n with its corresponding Fibonacci number. That is, whenever we calculate a value for F(n), we store the pair (n, F(n)) in our dictionary. Now, in the function call, we first check if n already exists in the dictionary (meaning it has been computed before). If it does, we return the stored value immediately. Otherwise, we make the normal recursive call, store the result in the dictionary, and then return it. This way, we avoid redundant calculations and improve the efficiency of the Fibonacci function. This process, in general, is called memoization, and it is an example of dynamic programming. Using memoization the tree becomes:

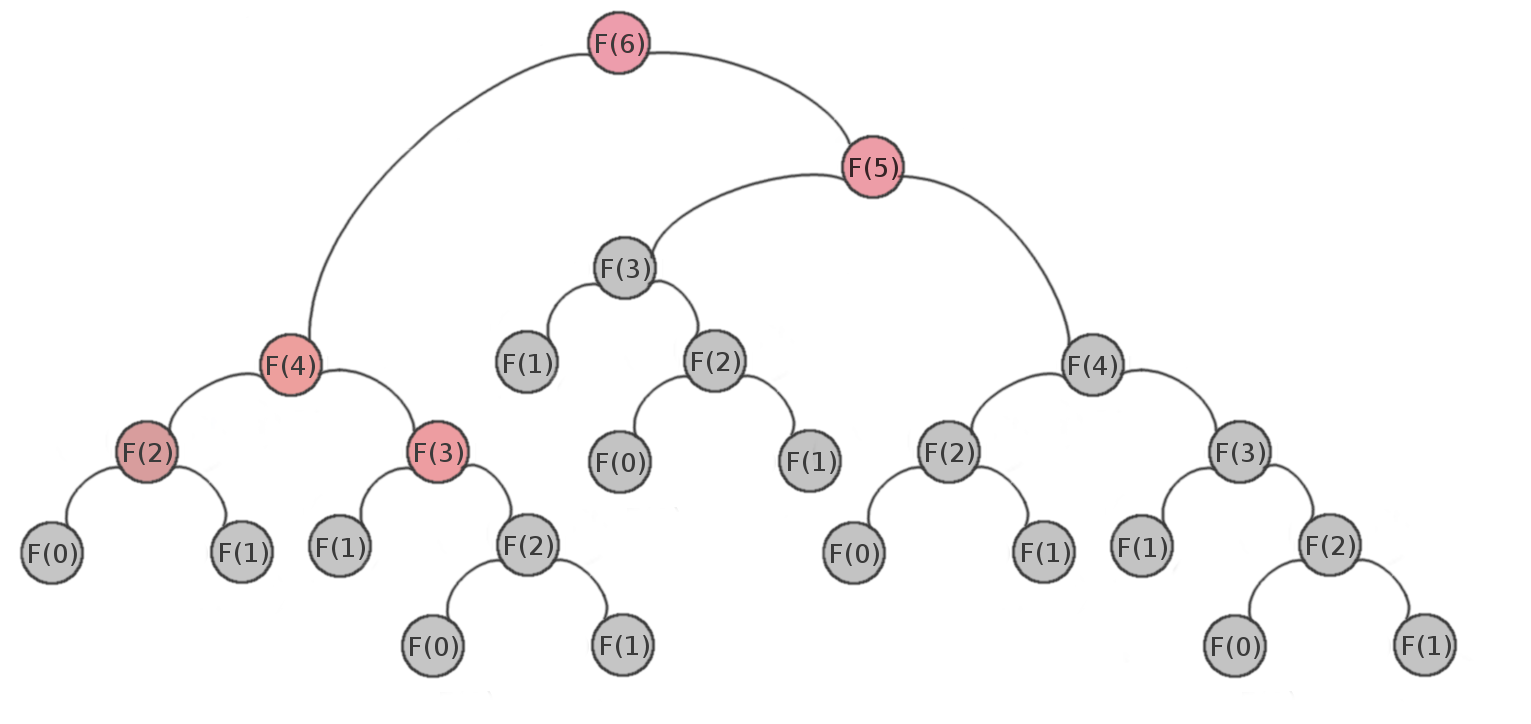
The grayed-out nodes are the ones which didn't need to be calculated; one of their parent's values was taken from the dictionary rather than being recalculated from scratch (i.e. the red nodes are the only calls where it's calculated). As you'll see in a while, the difference memoization makes is rather dramatic.

Your last task in this lab is to implement both the normal and memoized version of the fib function (in fib.cpp).

In C++, we can easily implement memoization using a static dictionary. The implementation is simple and straightforward. If you think you are ready to start implementing it right away, you can skip the next section. However, if you're interested in seeing an example of how to implement a memoized version of a recursive function in C++, you can refer to the next section where we explain a factorial function.

Memoized Factorials¶

This section is solely for demonstration purposes and serves as a refresher on recursion, as well as an example of memoization. We start with the recursive definition of the factorial: for a given input n, the factorial value, n! is always the same and is defined as:

0! = 1;
n! = n * (n-1)!

For example, say we already know the value of 5! and we want to compute 6!. The naïve way of computing 6! would be to calculate

6! = 6*(5*(4*(3*(2*(1))))).

Since we already know the value of 5!, however, we can save quite a bit of computation (and time) by directly computing:

6! = 6 * 5!

using the known value of 5!. This computation is thus using memoization. Now let’s write a C++ code to accomplish this. Take a look at the memoized_fac function in fac.cpp. On line 97, you find:

static map< unsigned long, unsigned long > memo = 
{
   {0, 1},
};

The left hand side is creating a variable named memo which is an std::map that associates keys of type unsigned long to values of type unsigned long. In our case, we’re going to map a key n to the value n!.

The static keyword is a neat little thing that basically makes this local variable remain initialized for the lifetime of the program so that we can reuse it across multiple calls to the function. It’s like a global variable, but it’s only accessible by that function.

The right hand side initializes the map to contain a key-value pair where the key is 0 and the value is 1. Notice that this key-value pair corresponds to the base case of our recursive definition of n! given above.

Alternatively, we could have used:

static map<unsigned long, unsigned long> memo;
memo[0] = 1;

The disadvantage of this method is that now the key 0’s value will be changed to the value 1 during EVERY function call, as opposed to just at initialization as in the first example.

Line 102 is:

auto lookup = memo.find(n);

memo.find(n) uses the std::map::find function. This method returns an iterator; the type of lookup is std::map<unsigned long, unsigned long>::iterator.

Lines 103-110 are:

if(lookup != memo.end()) {
    return lookup->second;
}
else {   
    unsigned long result = n * memoized_fac(n - 1);
    memo[n] = result;
    return result;
}

Going back to what we already know about iterators and std::map::find, a return value of memo.end() basically implies that the key n does not exist in the map. In this case, we need to compute n! and update our map to store that value, which is exactly what we do in the else branch.

Memoizing the factorial function actually doesn't do much for us in terms of computation time for a single . To see this for yourself you can run:

make fac
./fac 20

and compare it to the time it takes for the memoized version by passing the -m flag:

./fac 20 -m

Memoized Fibonacci Numbers¶

Memoization has a more noticeable impact on the speed of Fibonacci numbers computation compared to the factorial function. Once you implement both the recursive and memoized version of the fib function (in fib.cpp), you can race them with the fib_generator executable:

make fib_generator
./fib_generator 45

Then run:

./fib_generator 45 -m

to use memoization and experience the relative face-melting speed of dynamic programming.

Submitting Your Work¶

You can now upload your files in the box below. You need to submit exactly the 8 files you worked on to complete this lab:

anagram_dict.cpp
anagram_dict.h
cartalk_puzzle.cpp
common_words.cpp
common_words.h
fib.cpp
pronounce_dict.cpp
pronounce_dict.h

Before submitting, ensure that the output is as expected with no additional printing.

Note that the autograder randomizes the file contents, and the pronouncing dictionary is modified such that a fake homophone is added, so don't believe it! What matters is that the program does what it's told. This might take a while to process, so hang on!

Acknowledgments¶

We would like to express our gratitude to prof. Cinda Heeren and the student staff of the UIUC CS Data Structures course for creating and sharing the programming exercise materials that have served as the basis for the labs used in this course.

Revised by: Elmeri Uotila and Anna LaValle

Anna palautetta

Kommentteja tehtävästä?