Liukulukuesitys¶
Osaamistavoitteet: IEEE 754-standardin mukainen liukulukuesitys.
C-kieltä opiskellessa tutustuimme jo liukuluku-muuttujatyyppeihin float ja double. Käydäänpäs seuraavaksi läpi miten tietokone itseasiassa esittää ja käsittelee liukuluvut.
Liukuluku on tietokoneen tapa esittää reaaliluvut. Yleinen liukulukujen esitys tietokoneen muistissa perustuu IEEE 754-standardiin, jonka esityksen käymme läpi pääpiirteissään seuraavassa. Tarkka esitys asiasta kiinnostuneille löytyy toki oppikirjasta ja/tai netistä.
Mutta ennenkuin mennään asiassa pidemmälle, katsotaan ensin miten binääriluvuille esitetään desimaalit?
No, ihan vastaavasti desimaalipilkulla kuten kymmenjärjestelmässäkin. Kuvasta huomaamme, että desimaalipilkun/pisteen vasemmalla puolella olevat kakkosen potenssit ovat positiivisia ja oikealla puolen negatiivisia.

Esimerkkejä.
Binääriluku 10.101 = 1*2^1 + 0*2^0 + 1*2^-1 + 0*2^-2 + 1*2^-3 = 2 + 0 + 1/2 + 0 + 1/8 = 2.625 Binääriluku 101.01 = 4 + 0 + 1 + 0 + 1/4 = 5.25 Binääriluku 1010.1 = 8 + 2 + 1/2 = 10.5 Binääriluku 0.111111 = 0 + 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 = 63/64 = 0.984375
Huomataan, että pienin luku, jonka voimme valitulla bittimäärällä esittää, on LSB arvo.
Esimerkki. Yllä pienin luku olisi siis joko..
00.001 eli 2^-3 = 1/8 0.000001 eli 2^-6 = 1/64
Tästä syystä voimme binääriluvuilla vain arvioita reaaliluvuista valittuun tarkkuuteen asti. Arvioita voitaisiin tarkentaa kasvattamalla desimaaliosan bittimäärää, mutta ohjelmointikieli, tietokoneen muisti ja suoritinarkkitehtuurin tietysti rajoittavat tarkkuutta joka voidaan saavuttaa.
Esimerkki. Kokeile esittää reaaliluku 0.1 binäärilukuna, jossa desimaaliosa on 2 bittiä? Bittejä vastaavat desimaaliosat ovat 2^1 = 0.5 ja 2^2 = 0.25. Nyt ei voida esittää lukua 0.1 tarkasti. Tosin kun lisätään desimaaliosaan vielä bitti, jota vastaa lukua 2^3 = 0.125, päästään jo lähelle lukua 0.1.
Lisäksi, miten esität binääriluvuilla reaaliluvun, jota ei voi esittää 2:n kokonaislukupotensseilla (2^-n) valitussa tarkkuudessa.. esimerkiksi 1/3? Nyt binääriluku on yhtä päättymätön kuin peruskoulun matematiikassakin eli bittiesitykseen tulee toistoa, jolloin
1/3 = 0.01010101010101... Binääriluvun pyöristys¶
Samoin kuin desimaalilukuja, myös binäärilukuja voidaan pyöristää. Syy miksi asia esitetään tässä nyt, johtuu siitä että liukulukumuunnokset tietokoneessakin tekevät aika karkeita pyöristyksiä..
Esimerkki. Pyöristetään binääriluku lähimpään 1/4:n. Nyt pyöristystarkkuus mihin päästään on kaksi bittiä desimaaliosassa
.xx eli 2^-2 = 1/4. Valitaan binääriluku 100 puoliväliksi, jonka mukaan bittien pyöristys ylös- tai alaspäin tehdään. Pyöristysalgoritmi: Lähdetään purkamaan lukua pyöristystarkkuutta edeltävistä biteistä:
- Jos kahden viimeisen bitin xx edellä oleva bitti (eli puolivälin bitti) on
0xx, tällöin pyöristetään alaspäin. - Jos kahden viimeisen bitin xx edellä oleva bitti on
1xx, otetaan se mukaan pyöristykseen eli - Jos kolme bittiä 1xx ovat > 100, pyöristetään ylöspäin
- Jos kolme bittiä 1xx = 100, huomioidaan seuraava edellä oleva bitti
- Jos neljäs bitti on 1xxx, pyöristetään ylöspäin
- Jos neljäs bitti on 0xxx, pyöristetään alaspäin
Esimerkkejä. Pyöristys 2^2 = 1/4 tarkkuuteen, eli desimaaliosassa kaksi bittiä
.xx10.00011 // nyt kaksi viimeistä bittiä ovat 11 ja puolivälin 0,
// joten pyöristyy tarkkuudessa .xx alaspäin eli 10.00 (= 2.00)
10.00110 // nyt puolivälin bitti on 1 eli pyöristyy ylöspäin 10.01 (= 2.25)
10.11100 // pyöristyy ylöspäin, eli 11.00 (= 3.00)
10.10100 // pyöristyy alaspäin, eli 10.10 (= 2.50)
IEEE 754-liukulukustandardi¶
Ennenkuin kaivaudutaan standardien maailmaan, todetaan että liukuluvuille tietokoneissa/mikropiireissä on olemassa kaksi esitystapaa.
- Fixed-point-esitys: Nyt desimaalipisteen paikka on lyöty lukkoon, eli liukuluvun esityksessä on aina sovittu määrä desimaalibittejä. Tälläinen esitystapa on kätevä sikäli että se yksinkertaistaa laskentaa suorittavan logiikkapiirin toteutusta.
- Floating point (liukuva pilkku) -esitys: Nyt desimaalipisteen paikka "liukuu" tarpeen mukaan bittien välillä ja desimaalia kuvaavia bittejä on vaihteleva määrä. Tosin edelleenkin, johtuen rajoitetusta bittimäärästä, voimme esittää vain arvion desimaaliluvusta.
Nyt siis aiemmin esittelemämme tapa kuvata liukulukuja oli tyyppiä fixed-point ja nyt katsomme miten liukuvan pisteen esitys rakentuu.
Standardissa liukuluvun esitykseen kuuluu kolme osaa (käytämme tässä tietokoneelle sopivasti eksponentille kantalukua 2) :
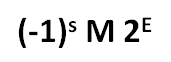
- Etumerkki s, jossa s=0 on positiivinen ja s=1 on negatiivinen.
- Mantissan M (murto-osa, engl. fractional) esitys
- M = 1 + xxx = 1.xxx, jossa
xxxvastaa murto-osaa. - Murto-osa etsitään binääriluvusta siirtämällä desimaalipistettä (molempiin suuntiin). Kts. esimerkki alla.
- Eksponentti E:n esitys
- E = exponent - bias
- bias = (2^(n-1))-1, jossa n on exponentin bittien määrä
- Yksinkertaisen tarkkuuden liukuluvuissa bias = 127 ja kaksinkertaisen tarkkuuden liukuluvuissa bias = 1023.
Esimerkki. Muunnetaan desimaaliluku 12345.0 float-tyypin liukuluvuksi.
Luku 12345.0 on binäärilukuna 11000000111001 * 2^0 (<-LSB) 1. Etsitään M siirtämällä desimaalipistettä vasemmalle: (Pilkkua siirtäessä desimaaliluvun pitää pysyä samana!) 11000000111001 * 2^0 = 12345.0 -> E=0 1100000011100.1 * 2^1 = 12345.0 -> E=1 110000001110.01 * 2^2 = 12345.0 -> E=2 ... 1.1000000111001 * 2^13 -> E=13 2. Lasketaan murto-osa M:n avulla. Pudotetaan luvun edestä kokonaisosa pois ja saadaan 1000000111001, johon lisätään 10 0-bittiä, jotta sen pituus on halutut 23 bittiä, -> murto-osa = 10000001110010000000000 3. Lasketaan exponentti: Kun E=13 ja bias=127, eli exponent = E + bias = 13 + 127 = 140 eli 10001100 4. Lopuksi etumerkki s=0, koska kyseessä on positiivinen luku.
Ylläolevan esimerkin tulos on siis:

Yllämainittu liukuluvun esitys on yleinen, esimerkkinä allaoleva pieni ja söötti (jap. kawaii) esitys 8:lla bitillä. Tässä bias = 7.

Lisäksi standardissa määritellään liukuvan pisteen liukulukuja kahta tyyppiä:
- Yksinkertaisen tarkkuuden liukuluvut (perustarkkuus, engl. single precision), jotka perustuvat on 32-bittiseen esitystapaan, merkkibitti +ja 8 eksponenttibittiä ja 23-bittiä murto-osaan.
- Kaksinkertaisen tarkkuuden liukuluvut (kaksoistarkkuus, engl. double precision), jotka perustuvat taas 64-bittiseen esitystapaan, eli merkkibitti ja 11 eksponenttibittiä ja 52-bittiä murto-osaan.
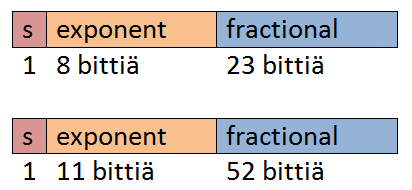
Selvää on että kaksinkertaisen tarkkuuden liukuluvuille lukualue on huomattavasti isompi ja tarkempi, mutta esityksen hintana on kasvanut muistin kulutus.
Erikoistapauksia¶
Koska IEEE 754-esityksellä ei voi esittää kaikkia lukuja, esimerkiksi nollaa (kokeile itse..), niin joudutaan määrittelemään muutama erikoistapaus.
- Nolla: exp = 000..0 ja frac = 000..0
- Ääretön: exp = 111..1 ja frac = 000..0
- NaN (not a number): exp = 111..1 ja frac erisuuri kuin 000..0
- NaN esittää tapaukset joita ei voi laskea, kuten sqrt(-1), ääretön - ääretön, jne..
Liukulukujen tarkkuudesta¶
Aiemmin todettiin, että liukuluku on aina arvio desimaaliluvusta ja lisäksi siinä on pyöristysvirhettä (engl. rounding error). Tarkastellaanpa asiaa ylläolevan söpön 8-bittisen liukuluvun esityksen kautta, koska pienellä lukualueella asiaa on helpompi visualisoida.
Kuvassa alla lukualue, kun exponentti on 4 bittiä ja murto-osa 3 bittiä. Nähdään että lukualue on tiivis lähellä nollaa, mutta harvenee lukujen suurentuessa. Alemmassa kuvassa tarkemmin lukualue lähellä nollaa.

-> Näinollen tästä esityksestä aiheutuva pyöristysvirhe on iso.
Muutetaan liukulukuesitystä niin, että exponentissa onkin nyt 3 bittiä ja murto-osassa 4 bittiä (bias on nyt 3) ja katsotaan mitä lukualueelle tapahtuu. Havaitaan että lukualue on kapeampi ja alue on tiiviimpi lähellä nollaa.

-> Muutoksen seurauksena pyöristysvirhe pienenee lukualueen sisällä.
Voidaan siis todeta, että liukuluvun lukualuetta voidaan kasvattaa lisäämällä bittejä exponenttiin ja liukuluvun tarkkuutta (erotuskykyä) kasvattaa lisäämällä bittejä murto-osaan. Mutta aina pitää huomioida aiheutuva pyöristysvirhe.
Hox! Asia voi tuntua vähäpätöiseltä, koska standardoidut lukualueet ovat varsin isoja ja tarkkoja, mutta ei olisi ensimmäinen kerta, kun tieteellisessä laskennassa tarkkuus ei riittäisi tai pyöristysvirheitä ei huomioitaisi..
Lopuksi¶
Nykyisin löytyy jo 32- ja 64-bittisiä isompia liukulukujen esitystapoja.
Liukuluvun esitys on käyty yksityiskohtaisesti läpi oppikirjassa. Kurssilla riittää, että ymmärrämme IEEE 754-standardin mukaisen esitystavan ja osaamme muuntaa liukulukuja esitysmuodosta toiseen.
Additional material¶
- You can have look to this interesting video where they explained how Quake programmers used IEEE754 float representation properties in order to simplify a complex math operation. Video was recommended by Eetu Vierimaa.